1-4 классы
1. Сколько кругов изображено на рисунке?
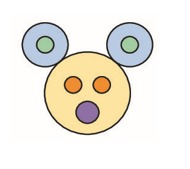
А) 5
Б) 6
В) 7
Г) 8
Д) 9
2. Кенгуру построили фигуру из пяти кубиков. Как Выглядит эта фигура, если смотреть на нее сверху?
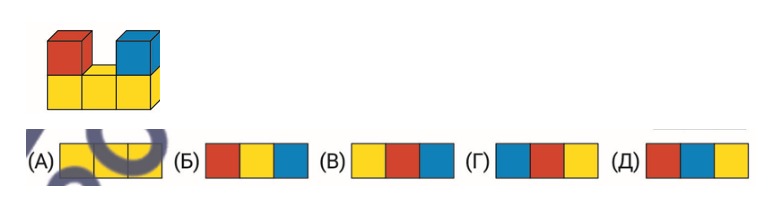
Ответ: Б
3. Имеется пять стеклянных ваз. В какой лежат шары с написанными на них номерами. В какой вазе сумма чисел на всех шарах наибольшая?

Ответ: А
4. Миша разрезал квадрат так. как показано на рисунке 1. Из получившихся кусочков он составил фигуру (рисунок 2). Какой из кусочков Миша не использовал, когда составлял фигуру?

Ответ: А
5. Петя нарисовал кораблик. На его кораблике нарисовано больше одного круга. Треугольников на нём на 2 больше, чем квадратов. Какой из корабликов нарисовал Петя?
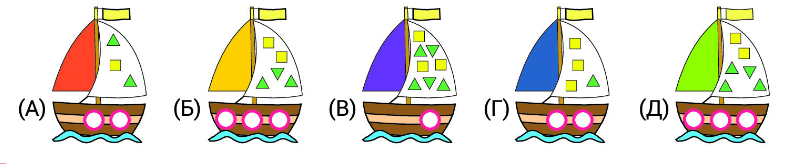
Ответ: Д
6. На каком рисунке фигуры не являются отражением друг друга относительно пунктирной линии?

Ответ: Б
7. У Вани было пять одинаковых свечей. Он зажёг их одновременно, а затем погасил каждую в своё время. После этого свечи стали выглядеть так, как показано на рисунке. Какую свечу Ваня потушил первой?
А) A
Б) B
В) C
Г) D
Д) E

8. В верном равенстве два одинаковых числа были закрыты квадратами со 20+10+10+?+?+1=51 знаками вопроса. Какие числа были закрыты?
А) 1
Б) 2
В) 5
Г) 10
Д) 20
9. Диск с двумя отверстиями накладывают на циферблат часов и вращают вокруг центра. Какую ещё пару чисел можно увидеть одновременно?

А) 4 и 9
Б) 5 и 9
В) 5 и 10
Г) 6 и 9
Д) 7 и 12
10.У Алисы есть четыре кусочка пазла. Какие два кусочка она должна сложить вместе, чтобы получить полный квадрат?
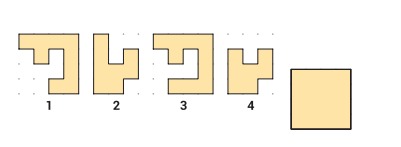
А) 1 и 2
Б) 1 и 3
В) 1 и 4
Г) 2 и 3
Д) 2 и 4
11. Светотехник в театре включает цветные прожекторы по такому плану:
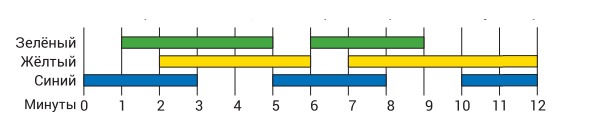
В течение первой минуты светит только синий прожектор. В последние две минуты светят жёлтый и синий прожекторы. Суммарно в течение скольких минут светят ровно два прожектора одновременно?
А) 2 минуты
Б) 6 минут
В) 8 минут
Г) 9 минут
Д)10 минут
5-8 классы
1. Валера заполняет таблицу числами от 1 до 40 подряд, как показано на рисунке. Какой кусочек он сможет вырезать из таблицы, когда заполнит её до конца?
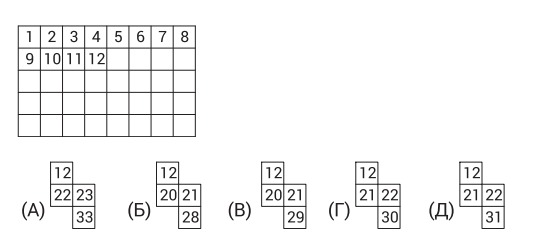
Ответ: В
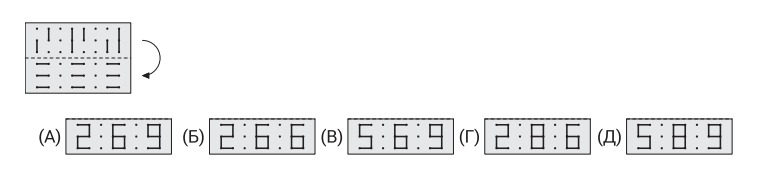
2.Кенгуру составляет числа из спичек. Цифры от 0 до 9 он всегда составляет так, как показано на рисунке. Например, чтобы составить таким способом число 15 или 8, ему потребуется семь спичек. Какое наибольшее положительное число кенгуру может составить из семи спичек?

А) 31
Б) 51
В) 74
Г) 711
Д) 800
3.У Иры есть развёртка, из которой она складывает кубик. Какой из следующих пяти кубиков у неё получился из этой развёртки?
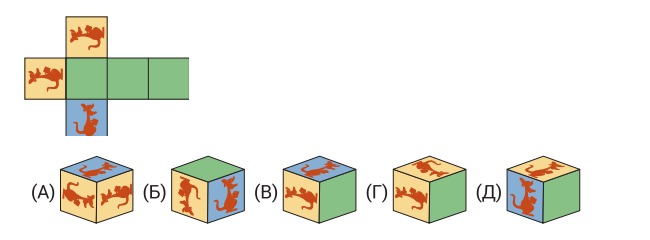
Ответ: Б
4.Альпинист взбирается по цилиндрической башне снизу вверх. Его путь отмечен на рисунке чёрным цветом. Все шаги альпиниста одинакового размера. Девять шагов видны на изображении. Сколько его шагов не видны?
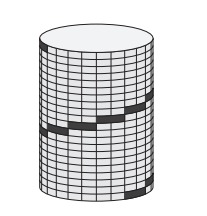
А) 9
Б) 10
В) 11
Г) 12
Д)13
5.У Саши есть пять дисков разных размеров. Он хочет построить такую башню из четырёх дисков, где каждый следующий диск меньше, чем предыдущий. Сколько различных вариантов таких башен Саша может построить?
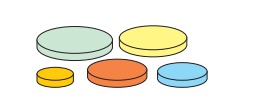
А) 4
Б) 5
В) 9
Г) 12
Д) 20
6.Решётка на рисунке состоит из вертикальных и горизонтальных линий. Одна часть этой решётки была скрыта. Какой из следующих кусочков является скрытой частью решётки?

Ответ: Б
7.Какую из следующих фигур нельзя разделить на две трапеции одной прямой линией?

Ответ: А
8. Диск с двумя отверстиями наложен на циферблат часов так, как показано на рисунке. Диск вращают вокруг центра до тех пор, пока в одном из отверстий не появится цифра 8. Какие два других числа возможно увидеть одновременно с ней?
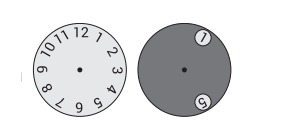
А) 4 или 12
Б) 1 или 5
В) 1 или 4
Г) 7 или 11
Д) 5 или 12
9. Коля хочет расставить по одному числу в каждой вершине ромба так, чтобы число, написанное на ребре, равнялось сумме двух чисел в вершинах, которые это ребро соединяет. Какое число должно стоять на месте вопросительного знака?

А) 11
Б) 12
В) 13
Г) 14
Д) 15
10.У Кристины есть кусок прозрачной плёнки с нарисованными на ней линиями. Она складывает его пополам, как показано на рисунке. Что она увидит?
Ответ: В
11. Мастер хочет выложить плиткой пол, используя плитки только одной формы. Зазоры и пропуски не допускаются. Плитка какой формы не может быть использована?

Ответ: Г
12. У Жени имеется 150 монет. Когда она бросила их на стол, 40% из них легли орлом вверх, и 60% — решкой вверх. Сколько монет, упавших решкой вверх, ей нужно перевернуть, чтобы количество монет, лежащих орлом вверх, и количество монет, лежащих решкой вверх, стало равным?
А) 10
Б) 15
В) 20
Г) 25
Д) 30
9-11 классы
1. По дороге в школу Маше пришлось бежать, чтобы успеть на автобус. Через две остановки она вышла и пошла дальше пешком. Какой из следующих графиков зависимости скорости от времени лучше всего представляет её дорогу до школы?
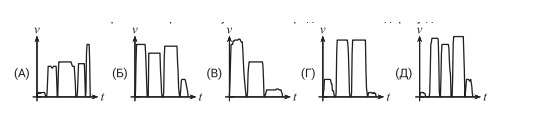
Ответ: Г
2. Целые положительные числа m и n являются нечётными. Какое из следующих целых чисел также является нечётным?
А) m(n+1)
Б) (m+1)(n+1)
В) m+n+2
Г) mn+2
Д) m+n
3. Внутри большого квадрата со стороной 10 см расположен меньший квадрат со стороной 4 см (смотри рисунок). Соответствующие стороны двух квадратов параллельны, и их центры совпадают. Какой процент площади большого квадрата закрашен серым цветом?

А) 35%
Б) 37%
В )40%
Г) 42%
Д) 45%
4.Сегодня четверг. Какой день недели будет через 2023 дня?
А) вторник
Б) среда
В) четверг
Г) пятница
Д) суббота
5.Прямоугольник ABCD составлен из 30 одинаковых квадратов. Периметр закрашенной фигуры равен 240 см. Чему равна площадь прямоугольника ABCD?
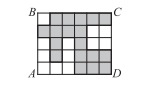
А) 1080 см2
Б) 1450 см2
В) 1580 см2
Г) 1920 см2
Д) 2430 см2
6. Семья состоит из пяти человек. Сумма их возрастов — 80 лет. Двум самым младшим членам этой семьи — 6 и 8 лет. Какова была сумма возрастов членов этой семьи 7 лет назад?
А) 35
В) 36
В) 45
Г) 46
Д) 66
7. Деревянный забор состоит из ряда вертикальных досок, каждая из которых соединена со следующей четырьмя горизонтальными досками. Первая и последняя доски в заборе вертикальные. Какое из следующих чисел может быть общим количеством досок в заборе?
А) 95
Б) 96
В) 97
Г) 98
Д) 99
8. В выражении a/5=7/b буквы a и b заменяют целыми положительными числами так, чтобы равенство было верным. Сколькими различными способами это может быть сделано?
А) 0
Б) 1
В) 2
Г) 3
Д) 4
9. После того как Вся выиграл 200 партий в шахматы, процент его побед составил 49%. Какое наименьшее количество дополнительных игр ему нужно выиграть, чтобы увеличить процент побед до 50%?
Ответ: Г
10. В каждой вершине треугольной пирамиде записано по целому положительному числу, а на каждом ребре указана сумма двух чисел, записанных в вершинах, которое это ребро соединяет. Какое число должно стоять на месте знака вопроса?
Ответ: Д
11. Женя решила экономить воду. Она сократила время, в течение которого умывается, на четверть. Она так же снизила напор воды, чтобы на четверть уменьшить скорость ее вытекания из крана. На какую долю Женя уменьшила общее количество воды, которое она использует для умывания?
А) 1/4
Б) 3/8
В) 5/8
Г) 5/12
Д) 7/16
12. На рисунке изображены три квадрата со сторонами 3 см, 5 см, 8 см. Какова площадь закрашенной фигуры?
А) 13 см^2
Б) 55/4^2
В) 61/4^2
Г) 65/^2
Д) 69/^2
13. Провод длиной 95 м разрезали на 3 части так, чтобы длина каждого следующего куска была на 50% больше, чем длина предыдущего. Какова длина самого большого куска провода?
А) 36 м
Б) 42 м.
В) 45 м.
Г) 46 м
Д) 48 м.
14. М и N — середины двух противоположных сторон прямоугольника. Какая часть прямоугольника закрашена?
А) 1/6
Б) 1/5
В) 1/4
Г) 1/3
Д) 1/2
15. У исследователя есть два сплава: первый сплав содержит 90% золота, а второй 54% золота. Он смешал 320 граммов первого и 160 граммов второго сплава, получив третий сплав. Сколько процентов золота содержится в получившимся сплаве?
А) 33%
Б) 48%
В) 65%
Г) 72%
Д) 78%
